https://padlet.com/milluans/jj7gpnxgbq7dy6zd
Matemáticas en casa ELA 2020
miércoles, 17 de noviembre de 2021
martes, 1 de diciembre de 2020
GESTIONAMOS RESIDUOS SÓLIDOS
SEMANA DEL 01 AL 04 DE DICIEMBRE
APRENDEMOS SOBRE LOS PRISMAS Y EL CILINDRO
Hola chicos y chicas, bienvenidos a nuestra semana 35 de trabajo remoto, esta SEMANA 35: GESTIONAMOS RESIDUOS SÓLIDOS, vamos a revisar un poco lo aprendido en las semanas 31 y 32 cuando elaboramos un cubo con ayuda de nuestros módulos Sonobé y recordarán que identificamos los elementos de un sólido geométrico: caras, aristas, vértices, ángulos diedros y diagonales.
Los residuos sólidos son desechos orgánicos e inorgánicos que se generan tras el proceso de fabricación,
transformación o utilización de bienes y servicios. Si estos residuos no se manejan adecuadamente,
producen contaminación ambiental y riesgos para la salud de las personas. esta semana trabajaremos bajo el título de GESTIONAMOS RESIDUOS SÓLIDOS porque vamos a reconocer formas geométricas de estos residuos que se desechan y muchos de ellos se gestionan porque deben ser separados para darles otro uso, por ejemplo los residuos orgánicos nos permiten elaborar abono para la tierra después de ser tratados adecuadamente. Otros residuos como de papel , cartón y plásticos pueden ser reciclados o reutilizados para otros fines.
Los residuos sólidos se producen en nuestra casa o departamento, en las oficinas, restaurantes, tiendas, empresas, etc. y afectan de sobremanera el ambiente. Una solución para contrarrestar este problema es la gestión de los residuos sólidos y para ello, se debe saber escogerlos, separarlos y almacenarlos, conforme a las normativas existentes para este tipo de residuos y, luego, trasladarlos al sitio de almacenamiento en camiones recolectores para proceder a su reciclaje o eliminación.
En estas actividades, establecerás relaciones entre las características y atributos medibles de objetos reales y representarás estas relaciones con formas tridimensionales (cilindros y prismas), considerando sus elementos y propiedades. Expresarás, con dibujos y con lenguaje geométrico, tu comprensión para interpretar un problema según su contexto y establecerás relaciones entre representaciones empleando recursos y procedimientos para determinar el área y volumen de figuras geométricas tridimensionales (cilindros y prismas) y plantearás afirmaciones sobre las relaciones y propiedades que descubrirás entre los objetos y formas geométricas.
Aprendamos un poquito sobre los prismas:
Después de haber visto el vídeo vamos ahora a resolver las siguientes situaciones:
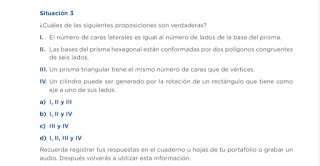
Como pueden ver los prismas llevan su nombre gracias a la forma de su base, si la base es un rectángulo se llamará prisma de base rectangular, y si fuese un triángulo será prisma de base triangular.
El número de caras de un prisma se obtiene contando el número de lados que tiene su base y se le agregan las dos bases.
Veamos ahora un poquito sobre el cilindro:
El desarrollo de un cilindro es un rectángulo cuyo lado más corto coincide con la altura del cilindro llamada también generatriz y su lado más largo del rectángulo equivale a la longitud de la circunferencia de su base.
Resolvamos las siguientes situaciones:
Podemos reforzar lo visto hoy con el siguiente programa de televisión:
Es hora de retar tu aprendizaje, recuerda que los sólidos geométricos son construcciones tridimensionales, podemos dibujar su desarrollo sobre papel pero debemos recortarlo y armarlo para que tenga las tres dimensiones (largo, ancho y altura). Utiliza tu imaginación para en tu mente visualizar las siguientes opciones:
jueves, 19 de noviembre de 2020
AYUDAMOS A ELIMINAR LA VIOLENCIA CONTRA NIÑAS Y MUJERES
SEMANA DEL 16 AL 20 DE NOVIEMBRE
ANALIZAMOS PORCENTAJES PARA ELIMINAR LA VIOLENCIA CONTRA NIÑAS Y MUJERES
Esta semana vamos a revisar el tema de los Porcentajes, si necesitas revisar un poco de información al respecto puedes ir a la SEMANA DEL 01 AL 05 DE JUNIO en este mismo blog, el título de la entrada es LOS PORCENTAJES.
Lo que corresponde a la presente semana son ejercicios de repaso sobre el tema, así que dejaré el enlace de la plataforma Aprendo en Casa para que la puedan visitar.
Igual avanzaremos juntos en nuestras sesiones en el grupo de whatsapp.
SEMANA DEL 23 AL 27 DE NOVIEMBRE
En estas actividades, establecerás relaciones entre datos y las transformarás en expresiones
numéricas que incluyen porcentajes y expresiones fraccionarias o decimales, expresarás
con diversas representaciones tu comprensión del porcentaje. Emplearás y combinarás
estrategias y procedimientos diversos para realizar operaciones con porcentajes, así como
la variación porcentual. Plantearás afirmaciones sobre los porcentajes y las justificarás
usando ejemplos y propiedades de los números y operaciones.
Seguiremos aplicando el tema de porcentajes en la resolución de situaciones problemáticas:
Como ya hemos revisado el tema por dos semanas , vamos al final a realizar nuestra autoevaluación.
martes, 3 de noviembre de 2020
USO DEL TIEMPO LIBRE
SEMANA DEL 02 AL 12 DE NOVIEMBRE
USO DEL TIEMPO LIBRE - MÓDULO DE SONOBE
Hola chicos y chicas, bienvenidos a nuestra semana 31y 32 de trabajo remoto, espero todos se encuentren bien en unión de sus familias.
Esta semana vamos a trabajar con la competencia "Resolvemos problemas de forma, movimiento y localización". No olviden colocar en sus respectivos portafolios SEMANA 31: USO DEL TIEMPO LIBRE.
¿QUÉ HAREMOS?
En estas actividades, establecerás relaciones entre las características y atributos medibles de objetos reales y representarás estas relaciones con formas bidimensionales. Construirás con material concreto, y expresarás con lenguaje geométrico tu comprensión sobre las propiedades del cuadrado y el triángulo. Asimismo, emplearás estrategias, recursos o procedimientos para elaborar las formas geométricas; y plantearás afirmaciones sobre las relaciones y propiedades que descubres entre ellas.
Seguro y en su entorno pueden identificar diferentes figuras geométricas (cuadrado, rectángulo, triángulo, círculo, etc) veamos cuanto recuerdan de ellas.
El triángulo es una figura de tres lados y 3 vértices. Es el polígono con el menor número de lados.
Un cuadrado es una figura de 4 lados iguales, que tiene 4 vértices (puntos que unen los lados en las esquinas) y 4 ángulos rectos ( ángulos que miden 90°)
El rectángulo es también una figura de 4 lados, 4 vértices y 4 ángulos rectos pero a diferencia del cuadrado solo sus lados paralelos son iguales, es decir sus lados que están frente a frente.
Existen otras figuras geométricas si quieres recordar más sobre ellas te dejo un enlace para que lo visites en tu tiempo libre, también puedes consultar en algún libro de matemáticas que tengas en casa, buscando el tema Las figuras geométricas.
Aquí les dejo un enlace que les puede ayudar:
Veamos la siguiente situación para opinar y resolver:
Situación 1
José corta piezas cuadradas de papel. Para comprobar si son cuadradas, mide los lados y verifica que sean iguales, después de lo cual, se asegura que están bien cortadas. En cambio, Alessandra dice que, para comprobar que las piezas de papel son cuadradas, se deben medir las diagonales; si estas son iguales, significa que la pieza cuadrada está bien cortada.
¿Estás de acuerdo con sus procedimientos para determinar si las piezas cortadas tienen forma cuadrada? Justifica tu respuesta.
Tanto José como Alexandra tienen razón para trazar su cuadrado, es cierto que los 4lados del cuadrado deben tener la misma medida y también es verdad que las dos diagonales de un cuadrado son iguales sin embargo hay algo que se les está pasando a ambos y es el hecho de que no pueden olvidar que los ángulos del cuadrado deben ser rectos y deben medir exactamente 90 grados.
Trazar un cuadrado en una hoja cuadriculada resulta sencillo pues podemos contar los cuadritos, trazar con la regla el contorno y recortar un cuadrado perfecto pero si queremos hacerlo en una hoja sin líneas es un poco más trabajoso. Para que sea perfecto el cuadrado podemos ayudarnos de instrumentos de dibujo como regla, compás, lápiz, escuadras, transportador para obtener la precisión que necesitamos.
Veamos el siguiente vídeo:
Genial, vamos a elaborar 10 cuadrados perfectos con el material que les había solicitado, ellos nos servirán para nuestro siguiente trabajo.
¿QUÉ HAREMOS LUEGO?
Usar nuestros conocimientos matemáticos puede ser de gran utilidad al buscar actividades creativas, dinámicas y recreativas para nuestro tiempo libre. Por ejemplo, podemos crear con materiales reciclables objetos de formas tridimensionales, como: llaveros, adornos, etc.
Utilizando los módulos atribuidos al japonés Mitsunobu Sonobe, tendremos como objetivo construir adornos de formas geométricas tridimensionales.
¿QUE ES EL MODULO DE SONOBE?
El módulo Sonobe es una de las muchas unidades que se utilizan para construir origami modular.
Se desconoce el origen del módulo Sonobe. Dos posibles creadores son Toshie Takahama y Mitsunobu Sonobe, quienes publicaron varios libros juntos y ambos miembros del Grupo Sosaku Origami 67. Sin embargo, la primera aparición de un módulo Sonobe fue en un cubo atribuido a Mitsunobu Sonobe en un libro del Grupo Sosaku Origami publicado en 1968. no revela si inventó el módulo o utilizó un diseño anterior: la frase "modelo terminado por Mitsunobu Sonobe" es ambigua. Su siguiente aparición fue "Toshie's Jewel", que apareció en 1974. Sin embargo, ninguna de las carpetas aprovechó todo el potencial del módulo. Este potencial fue descubierto en la década de 1970 por otras carpetas, en particular Steve Krimball, quien creó la bola de 30 unidades, como parte de un período repentino de desarrollo en el origami modular.
Veamos como se construye un módulo Sonobe y lo haremos con los 10 cuadrados que tenemos.
Entonces, la SITUACIÓN 1 para hoy es elaborar el módulo SONOBE con los 10 cuadrados que recortaste ayer, es que se necesita 10 piezas al menos para construir algo con ayuda del módulo, así que tendremos listas las piezas para la próxima semana.
Situación 2
¿Qué formas geométricas bidimensionales reconoces en el módulo de Sonobe?
Representa mediante un dibujo un triángulo que identificaste en el módulo de Sonobe.
Justifica qué tipo de triángulo es y determina sus elementos.
Igual te dejo un enlace para que encuentres mas información para el logro de tus retos.
Continuamos con las actividades que involucran el módulo de Sonobè.
En estas actividades, estableceremos relaciones entre las características y atributos
medibles de objetos o formas geométricas, estas relaciones las representaremos
con formas geométricas bidimensionales o tridimensionales, y describiremos sus
características, propiedades y elementos. Asimismo, construiremos cubos y pirámides
e identificaremos sus elementos, características y sus propiedades; finalmente,
justificaremos enunciados haciendo uso de nuestros conocimientos matemáticos.
Ya tenemos 10 de ellos armados y listos para usarlos en la construcción de una forma tridimensional, esta vez será primero un cubo y luego una pirámide.
Veamos con atención el siguiente vídeo para paso a paso lograr nuestro reto.
Además con ayuda del video vamos a conocer sobre el cubo y dar respuesta en nuestro portafolio a las siguientes interrogantes:
1. ¿Cuántos vértices y aristas tiene el cubo?
2. ¿Cuántas caras tiene el cubo?
3. ¿Cuántas dimensiones tiene la figura de una cara del cubo?
4. ¿Cuál es el área de las caras laterales del cubo?
5. ¿Cuántas dimensiones tiene el cubo?
6. ¿Cuál es su volumen?
7. Si dividimos un cubo por su diagonal , ¿qué sólido geométrico se forma?
8. Describe las características del cubo.
miércoles, 28 de octubre de 2020
CUIDAMOS NUESTRA SALUD INTEGRAL II
SEMANA DEL 26 AL 30 DE OCTUBRE
CUIDAMOS NUESTRA SALUD INTEGRAL
Continuamos con nuestro trabajo de las probabilidades. No perdamos de vista lo siguiente:
La probabilidad se expresa como un cociente, es decir una división, en donde dividimos la cantidad de casos favorables entre el total de casos posibles (REGLA DE LAPLACE), al escribir esta fracción (división) también podemos dividir el numerador entre el denominador y encontraremos la probabilidad expresada como un decimal, es conveniente que este decimal se escriba con dos cifras decimales, es decir aproximado hasta las centésimas pues así podemos multiplicarlo por 100 de manera más rápida y obtendremos la probabilidad expresada como un porcentaje.
Podemos revisar los vídeos publicados la semana pasada si necesitamos reforzar las ideas principales del tema antes de desafiar nuestro aprendizaje con dos situaciones retadoras.
Vamos analizando la situación:1. ¿Del 0 al 99 cuántas bolitas hay?
2. Entre estas 100 bolitas numeradas ¿Cuáles tienen un 3 en su numeración?
¿cuántas son?
3. Entonces si de las 100 hay 19 que incluyen a la cifra 3, ¿cuántas no incluyen la cifra 3 en su numeración?
4. Muy bien serían 81 bolitas, entonces ¿cuál es la probabilidad para Juan?
Ahora María quiere que las bolitas que se extraigan no tengan la cifra 9 en su numeración ¿Cómo lo harías? ¿Cuál sería la probabilidad para María?
Ahora responde, ¿Quién tiene mayor probabilidad de lograr su objetivo? ¿Juan o María?
Veamos una siguiente situación:
Pues bien, veamos qué pasa cuando lanzamos las tres monedas al mismo tiempo, qué opciones tenemos...Como pueden ver tenemos 8 combinaciones diferentes posibles de obtener al lanzar las tres monedas.
Ahora observen con atención y me dicen cuántas de esa opciones me dan tres caras...
Sólo hay una verdad?? Eso quiere decir que la probabilidad de obtener tres caras al lanzar tres monedas al mismo tiempo es 1/8
Y cuántas opciones tienen dos sellos y una cara?
Muy bien tenemos dos opciones de las 8 posibilidades eso quiere decir que la probabilidad de sacar dos sellos y una cara al lanzar las tres monedas es 2/8
Por lo tanto qué es más probable para César?
Excelente!!! Hicieron un gran trabajo. Evaluemos lo que hicimos para estar seguros de haber logrado lo que se quería:
miércoles, 21 de octubre de 2020
CUIDAMOS NUESTRA SALUD INTEGRAL
SEMANA DEL 19 AL 23 DE OCTUBRE
CUIDAMOS NUESTRA SALUD INTEGRAL
El azar está presente en la vida cotidiana, existen muchos contextos en los que aparecen la incertidumbre,
el riesgo y la probabilidad. Por ejemplo: el pronóstico del tiempo, el diagnóstico médico, la posibilidad
de requerir un seguro oncológico o de obtener utilidades al efectuar una inversión, entre otros.
La posibilidad de que suceda un hecho o acontecimiento de un conjunto de posibles resultados, se
expresa matemáticamente por la probabilidad.
Si tienes alguna dificultad para realizar la actividad solicita el apoyo de un familiar.
¿QUÉ HAREMOS?
En estas actividades, determinarás las condiciones de una situación aleatoria y representarás la probabilidad de algunos sucesos a través de la regla de Laplace y, a partir de este valor, determinarás si un suceso es más o menos probable que otro. Asimismo, expresarás con diversas representaciones y lenguaje matemático tu comprensión sobre el valor de la probabilidad. También, emplearás diversas estrategias
para determinar la probabilidad de sucesos simples y plantearás afirmaciones y las justificarás con tus conocimientos.
¡ATENTA/O!, QUE AQUÍ ENTRAMOS DE LLENO AL DESARROLLO
Acomódate en el espacio de tu casa asignado para realizar con tranquilidad tus actividades. Recuerda lavarte las manos y desinfectar los materiales que utilizarás.
A continuación, te invitamos a seguir desarrollando la siguiente situación:
Observa con atención las urnas, contabiliza cuántos tickets tienes en cada una de las urnas, esas cantidades representan tu espacio muestral para cada una de las urnas. Luego lee con atención cada una de las preguntas e iremos hallando las respectivas probabilidades.
Veamos una nueva situación:
Vamos a ver qué sucede cuando lanzamos una moneda dos veces, observa con atención y responde la pregunta del problema.
Finalmente veamos un nuevo vídeo para reforzar lo visto hasta el momento.
Ahora es el momento del reto, espero haberte ayudado y puedas resolver estas dos situaciones.
martes, 13 de octubre de 2020
CONSERVAMOS Y PROMOVEMOS NUESTRA BIODIVERSIDAD II
SEMANA DEL 12 AL 16 DE OCTUBRE
Vamos a revisar un poco lo que trabajamos la semana pasada sobre los números enteros, ya hemos identificado varias situaciones reales en las que los números enteros se pueden utilizar, inclusive hemos resuelto situaciones problemáticas con ayuda de los enteros, pero ¿qué contenidos matemáticos hemos utilizado?
Veamos:
1) Los números enteros son un conjunto que incluye a los números naturales, aquí se llaman enteros positivos. En los Enteros tenemos el cero, que se ubica al centro de la recta numérica y tenemos los enteros negativos hacia la izquierda del cero y los enteros positivos hacia la derecha del cero.
2) Todo entero tiene un opuesto es decir el mismo número pero con signo contrario. Por ejemplo
-20, su opuesto es +20
+3 , su opuesto es -3
3) El único entero que no tiene opuesto es el cero porque él no tiene signo
4) El valor absoluto de un entero es la distancia que existe desde ese número hasta el cero, como hablamos de una distancia el valor absoluto siempre es positivo y se escribe como el mismo número pero sin signo. Veamos
-7 , su valor absoluto es 7
+34 su valor absoluto es 34
-18 su valor absoluto es 18
También podemos trabajar operaciones con enteros, revisemos la adición y sustracción:
Ahora en nuestro portafolio vamos a resolver las siguientes situaciones, trata de ser muy ordenado. No olvides escribir el título SEMANA 28: CONSERVAMOS Y PROMOVEMOS NUESTRA BIODIVERSIDAD
Recuerda que el reto de la semana es resolver situaciones problemáticas que involucran operaciones con números enteros.
Recuerda que puedes utilizar tu propia estrategia de trabajo (dibujar en la recta, dibujar un termómetro, o simplemente sumar o restar enteros). ya sabes leemos bien el problema para comprenderlo, planeamos y aplicamos nuestra estrategia y finalmente comprobamos nuestros resultados.
También podemos ver el programa de TV para comprender más el tema, aquí dejo el enlace https://www.youtube.com/watch?v=4LJ0qL61y0c&t=1047s
Ahora vamos a trabajar nuevas situaciones que involucran a los números enteros y para ello vamos a recurrir a dos nuevas operaciones, la multiplicación y la división, veamos como trabajan ellas...
Si ya viste el vídeo has observado el uso de la ley de signos para multiplicar y dividir enteros, vamos a aplicar lo aprendido resolviendo las siguientes situaciones:
Aquí dejo algo adicional para ti, si gustas puedes involucra a tu familia para que juntos encuentren la solución
También puedes mirar el siguiente vídeo para reforzar lo aprendido....................
Suscribirse a:
Comentarios (Atom)